Something I have been (occasionally) thinking about for quite a long time is the means to manipulate high-dimensional data-sets (dense grids, specifically), and do so efficiently. Namely, I wish to make the data along any specific orthgonal basis direction to become adjacent in memory by strides of the length of samples along that axis.
The reason for this? To allow for optimal vectorisation and caching of data when performing computations. Take for example a GPU: if we put data on GPU memory we want to access and manipulate it in chunks given by the chosen thread-size. If we access elements out of order, we essentially lose all of the parallelism offered by the device, as the data access will not be performed in the optimal $n$-element wide chunks, but individually at worst, and somewhere in between most likely.
For a problem with a Cartesian gridded data set in the space given by $ijk$, we can define the lexicographical order from fastest to slowest indices to be in the $ijk$ order.
for(int k=0; k < k_size; ++k)
for(int j=0; j < j_size; ++j)
for(int i=0; i < i_size; ++i)
data[i + i_size*(j + j_size*k)] = 0;
In this example, $i$ is the fast index and the axis along which the data is linearly adjacent in memory, and $k$ is the slow axis (with $j$ being slower than fast and faster than slow).
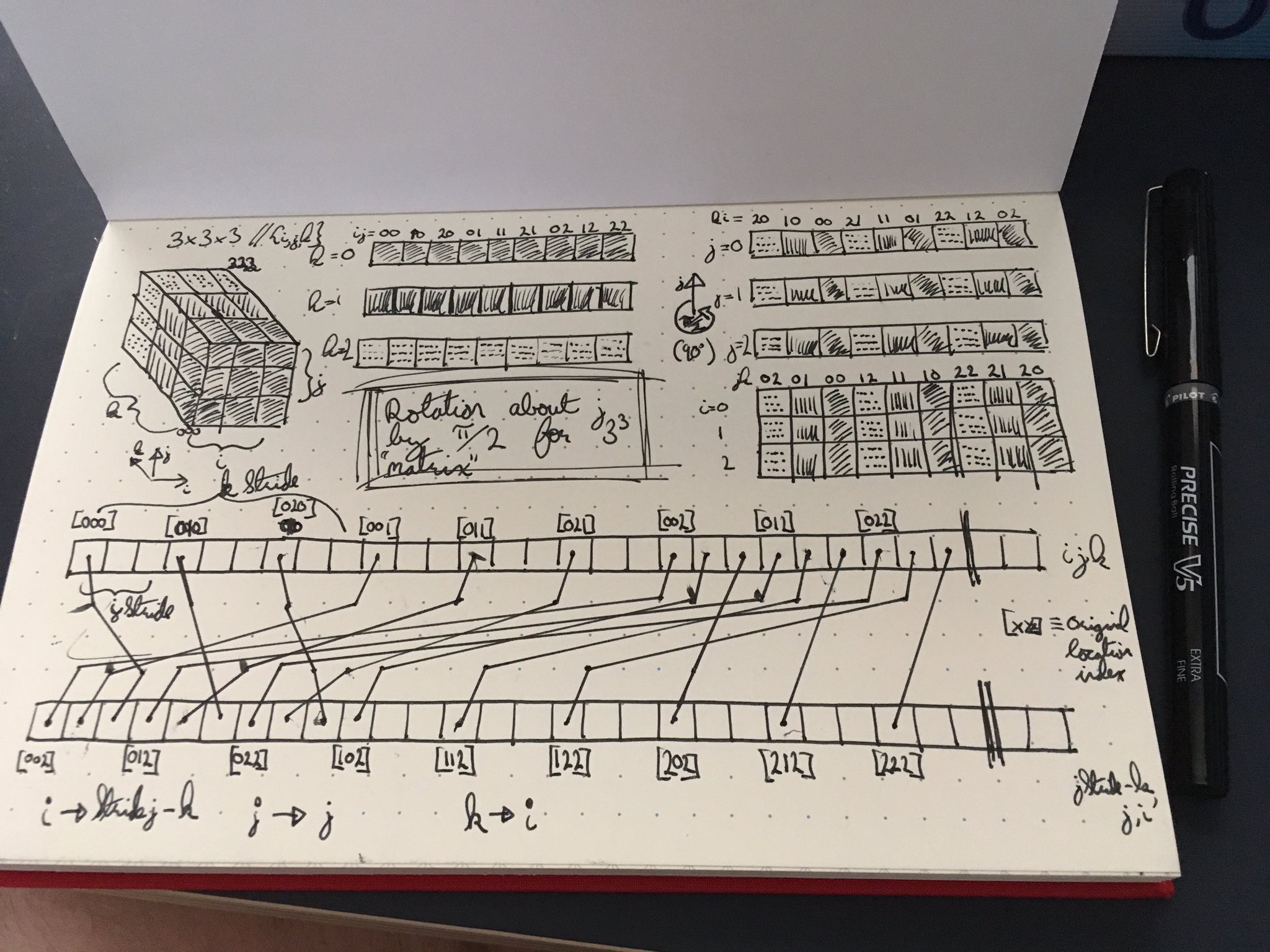
The included image above is an example of rotation about the $j$ axis, showing on the right the respective mappings to new index values (for the sake of my interest I’ve taken slices along $j$ and $i$, but worked with the latter for the rest of this discussion).
The bottom of the image shows the rearrangements of memory from the original (upper) to the rotated (lower) memory configurations. The indices themselves seem to take the following mappings (orig. $\rightarrow $ rot.):
$$ \begin{align}
i & \rightarrow \textrm{stride}(j)-k, \\
j & \rightarrow j, \\
k & \rightarrow i, \
\end{align}$$
where the stride() operation returns the spacing between the elements in the given dimension (in this case, the stride of $j$ is the size of $i$).
I intend to find an optimal way to perform this in time. Even suboptimal, but good enough would be fine though.
L.